Mathematical brains — an excerpt from ‘Seeing the Mind’
In this series of essays, newly published in English, cognitive neuroscientist Stanislas Dehaene taps brain images to help explain new findings.
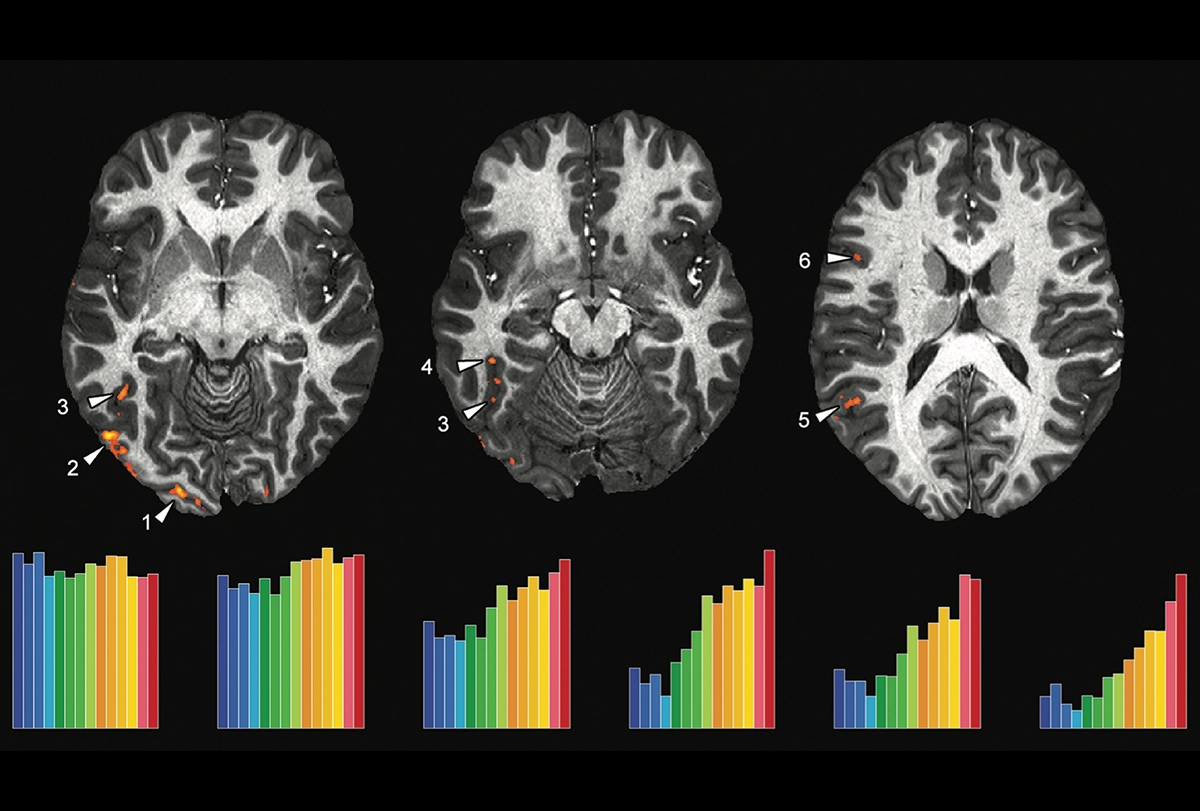
How do human neurons get tuned to reading? We don’t know yet, but thanks to the increasing power of its magnetic field, we can use MRI to zoom in on the portions of the cortex that activate during reading, and try to understand what excites them.
The images you see here were acquired at a scale of 1.2 millimeters using NeuroSpin’s 7-tesla MRI machine. Unlike most previous images, they represent not the average of a few dozen people, but the brain of a single volunteer. Unblurred, they show the reading circuit with unprecedented resolution.
First surprise: What previously seemed to be a vast region engaged in reading has exploded into a constellation of scattered patches. It is as if, by deploying a new telescope, we discover that what we thought was a star is actually a galaxy. The new images suggest that reading mobilizes tiny specialized areas. This is exactly what has been observed for face recognition: A small number of cortical patches contain up to 98 percent of neurons entirely dedicated to faces. Similar learning rules probably govern the acquisition of reading and face recognition.
Second surprise: These regions accumulate statistics on written words, regardless of language. The person you see here is bilingual in English and French. However, their brain does not contain any region dedicated to only one of these languages. Instead, the two writing systems overlap. What matters to the brain is not which language is written, but whether a sequence of letters respects the statistics of the languages that the person can read.
Here, we manipulated those statistics continually by presenting stimuli ranging from completely implausible strings, made of rare letters, to reasonable ones that might be real words — and some actually were. In the visual areas of occipital cortex, all of those stimuli evoke the same activity: Only the lines they contain matter. However, higher up into the cortex, we begin to see a specialization in favor of the known languages. In the temporal cortex, and even more so in Broca’s area, a sequence of letters must look like a plausible word in order to excite the neuronal circuits for reading.
Thus, with experience, human neurons probably become tuned to the statistics of writing. I speculate that the cortex of all good readers houses neurons tuned to frequent letters, common letter pairs, word roots and perhaps even entire words — a prediction that could ultimately be tested once we manage to record from single cells in humans.
Reading is just one example; in all domains, our brain acts as a statistician that accumulates observations and uses them to refine its internal models of the world.
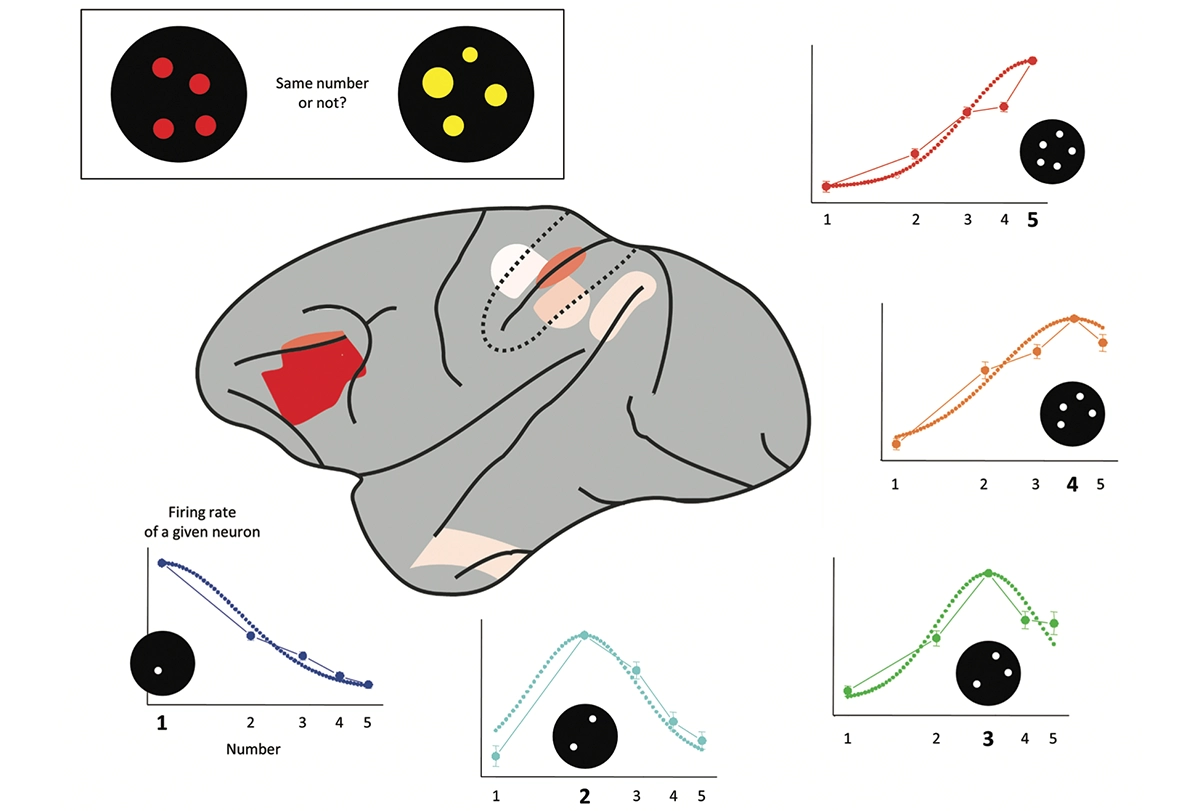
How many: Macaque monkeys’ brains have number neurons. The regions in red, in the prefrontal and parietal cortex, contain a large proportion of neurons tuned to a given number of objects, here between one and five. The research was carried out by Andreas Nieder and his colleagues, first at the Massachusetts Institute of Technology and then at the University of Tübingen in Germany.
Number Neurons
Learning to read is clearly the prerogative of the human species, but what about mathematics? Is basic math accessible to other animals? To find out, Andreas Nieder and Earl Miller examined whether macaque monkeys understand the concept of number. They trained them on a same/different judgment: On each trial, the animal saw two sets of objects, one after the other, and had to decide whether they shared the same number.
First finding: After some training, the monkeys performed this task remarkably well. They succeeded with a great variety of configurations, and could clearly focus solely on number. Their only problem was to answer “same” when the two numbers were close, like 4 and 5. Thus, monkeys cannot count but can only estimate an approximate quantity of items.
Second finding: The macaque brain contains neurons tuned to number. Each of these cells responds to a certain number of objects. Some fire only when the animal sees one object; others prefer two; still others are stimulated by seeing three, four, or five objects. Each neuron possesses a favorite number, but their tuning is not perfectly sharp: Neurons that fire the most to four objects, for example, also respond to three or five objects. Again, monkeys’ number sense is approximate.
A similar number sense is present in humans. We too are capable of estimating a number without counting, and our parietal cortex contains a number map with different sectors tuned to different quantities of objects. Single neurons similar to those of monkeys have even been found in the human hippocampus.
None of this, by the way, is unique to primates. Many species, without any special training, pay attention to the numbers around them. Number neurons virtually identical to those of monkeys have even been observed in crows. Basic arithmetic is so useful for survival, whether to find as much food as possible or to check how many conspecifics are in a coalition, that many distinct animal lineages seem to have evolved the same sort of brain circuit for number sense; alternatively, number may be such a fundamental concept that the brain has paid attention to it for hundreds of millions of years.
Is there nothing special, then, about us humans? Of course there is: We are the only animal that manages to overcome the fuzziness of this approximate number sense. Using symbols, we develop a precise and rigorous arithmetic that serves as the foundation for the edifice of mathematics. The acquisition of a language of mathematics considerably amplifies the initial potential of our brain.
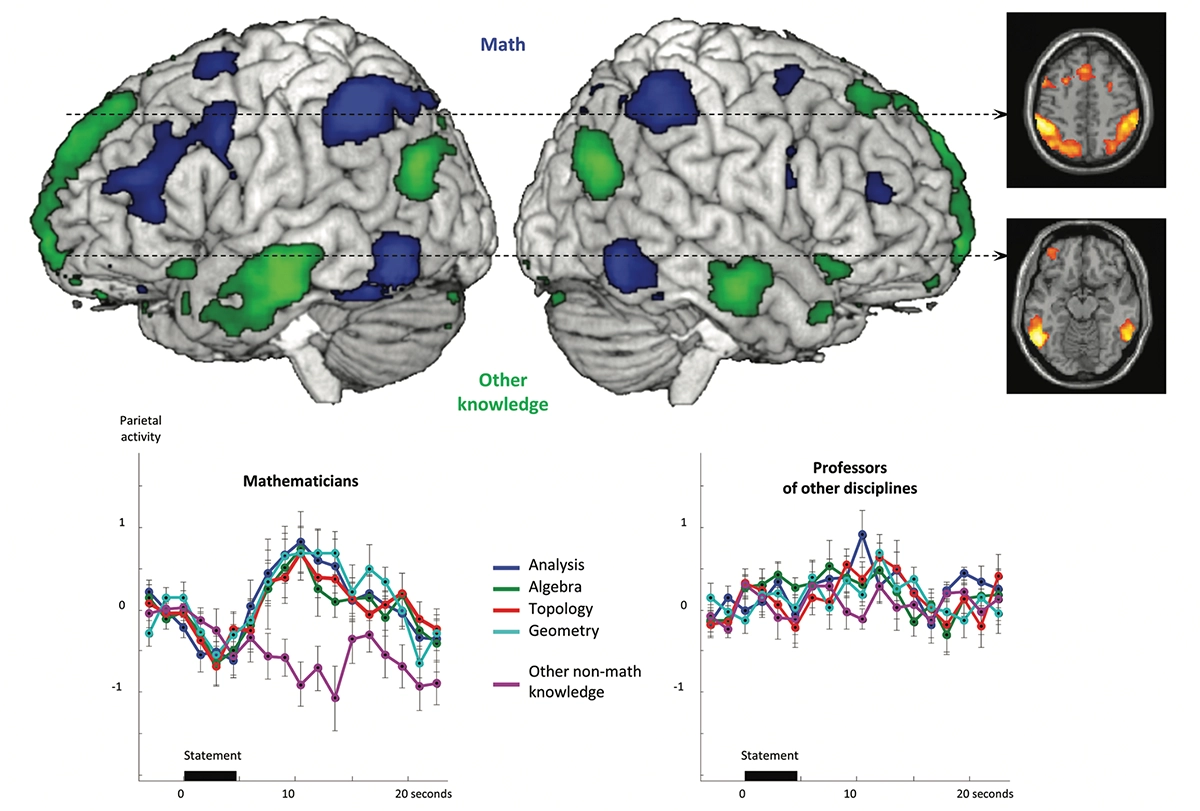
Mathematical minds: These scans show activity evoked by mathematical and nonmathematical statements in the brains of professional mathematicians. Marie Amalric and the author conducted the work at the NeuroSpin Center in Saclay, France.
The brains of mathematicians
What happens in the brains of those who learn mathematics? Do great mathematicians develop specific brain circuits? Which areas of the cortex allow them to think about infinite-dimensional vector spaces, imaginary numbers or group theory?
To answer those questions, Marie Amalric and I conducted the first systematic brain-imaging experiments of professional mathematicians. Lying in NeuroSpin’s 3-tesla MRI scanner, they would hear sentences such as “The Euclidean orthogonal group has exactly two connected components” and had to decide whether they were true or not (this one is true, but to nonmathematicians, it is far from obvious). Other sentences, of equal difficulty, assessed nonmathematical knowledge, for example, “The end of the Council of Trent coincides with the fall of the Western Roman Empire” (this is false).
The results showed that the brain uses completely different areas to store mathematical and nonmathematical knowledge. When a mathematician thinks about math — whether it is analysis, algebra, geometry or topology — the parietal and inferior temporal regions of both hemispheres light up. A completely different set of regions, notably, the temporal pole and the angular gyrus, encode other types of semantic knowledge. The mathematician’s brain therefore houses a specialized circuit for mathematical knowledge.
In our experiment, mathematicians activated these regions when listening to mathematical sentences, but this was not the case for the humanities and social sciences teachers who listened to the same statements. Does this mean that mathematicians possess a radically different cortical organization than the average person? Not at all: The regions for mathematics are present in each of us. All it takes to activate them are much simpler sentences such as “How much is two times three?” or “Any number multiplied by zero is zero.” In fact, these areas have been around for a long time in evolution: They are the same ones that light up when a macaque monkey evaluates an approximate quantity of objects.
In a nutshell, learning mathematics recycles a circuit that has existed for millions of years, and which is already interested in numbers and space. However, only the human species, with its remarkable knack for language and symbols, manages to build, on top of this ancient foundation, a pyramid of concepts of increasing abstraction: whole numbers, decimals, fractions, operations, functions, infinite spaces and other concepts.
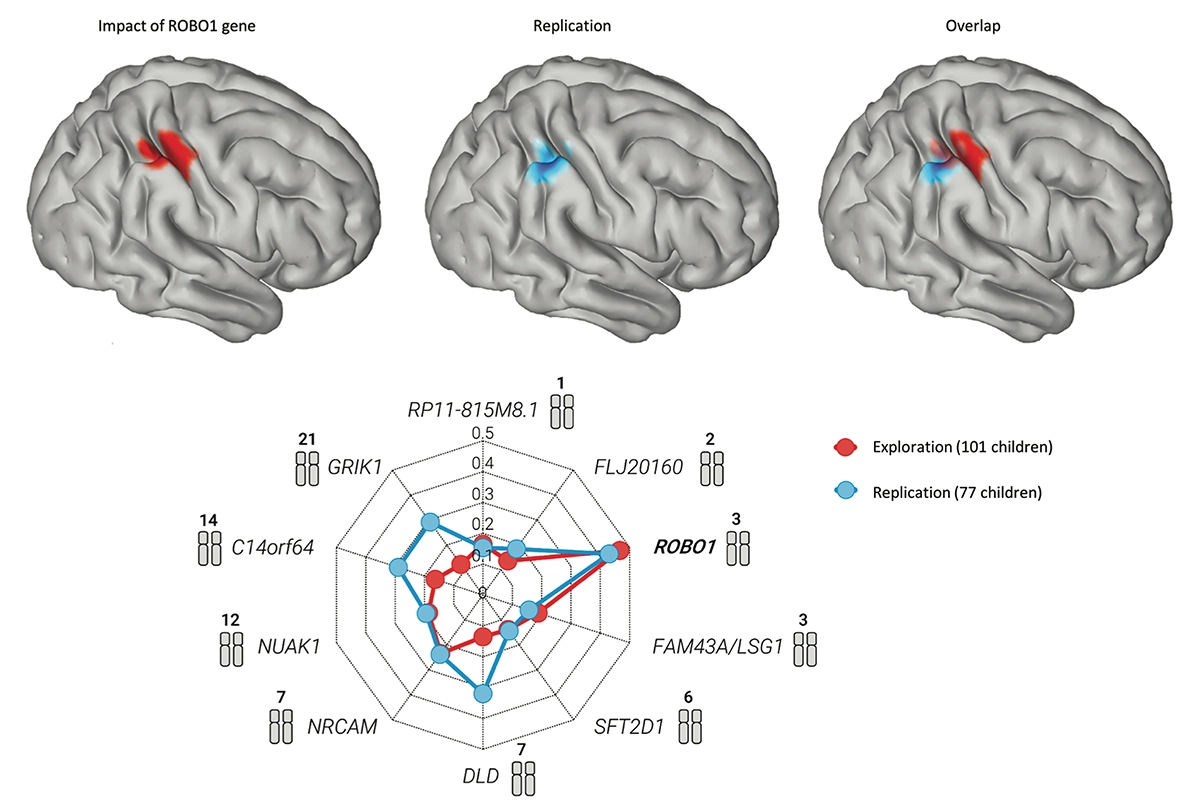
A knack for math: Polymorphisms of the ROBO1 gene modulate cortical regions, shown here in children aged 3 to 6 years, and mathematical skills. Michael Skeide and his collaborators at the Max Planck Institute in Leipzig, Germany, conducted the work.
Are you a math whiz?
“Arithmetic, algebra, geometry, awe-inspiring trinity, luminous triangle! He who has not known you is a fool!”
—Comte de Lautréamont, The Songs of Maldoror (1868–1869)
Why is it that some people, like Lautréamont, adore mathematics, while others hate it? Education plays a major role: All human brains, if they go to the right school, can learn to master questions that, in ancient times, stood up to the greatest mathematicians.
Genetics also comes into play. Mathematical skills are partly heritable: Identical twins tend to share the same talents, even if they are raised under different conditions. Conversely, some genetic diseases, particularly when they affect the parietal lobe, are associated with disorders of mathematical operations, or dyscalculia. However, no gene specifically associated with mathematics has yet been identified with certainty.
In the study illustrated here, the researchers examined the impact of 10 candidate genes on the brains of children aged 3 to 6 years. Previous studies had suggested that, at those 10 sites on the genome, variations across individuals correlated with developmental impairments in the domains of number and space. Brain imaging confirmed that, in two different groups, the alleles of the ROBO1 gene modulated the thickness of the cortex in the right intraparietal region. This thickness, in turn, predicted about 10–20 percent of the variance in school grades in mathematics between the ages of 7 and 9.
This result makes sense: Not only is the intraparietal sulcus a core region that activates as soon as we think about numbers and math, but it lights up most clearly in the right hemisphere of children and newborns. From birth, in fact, all children possess a number sense, the ability to assess, without counting, the number of a set of objects — and this innate ability seems to be associated with the right parietal region.
In brief, we all share a knack for math, but it is modulated by genetic variants, including those of the ROBO1 gene. Dozens of other genes are also likely to be involved. If the genetics of cognitive functions is still in its infancy, it is undoubtedly because the effects of genes and education are irremediably intertwined. We should not overestimate the power of genes: Their effects are real, but they are dwarfed by the power of education.
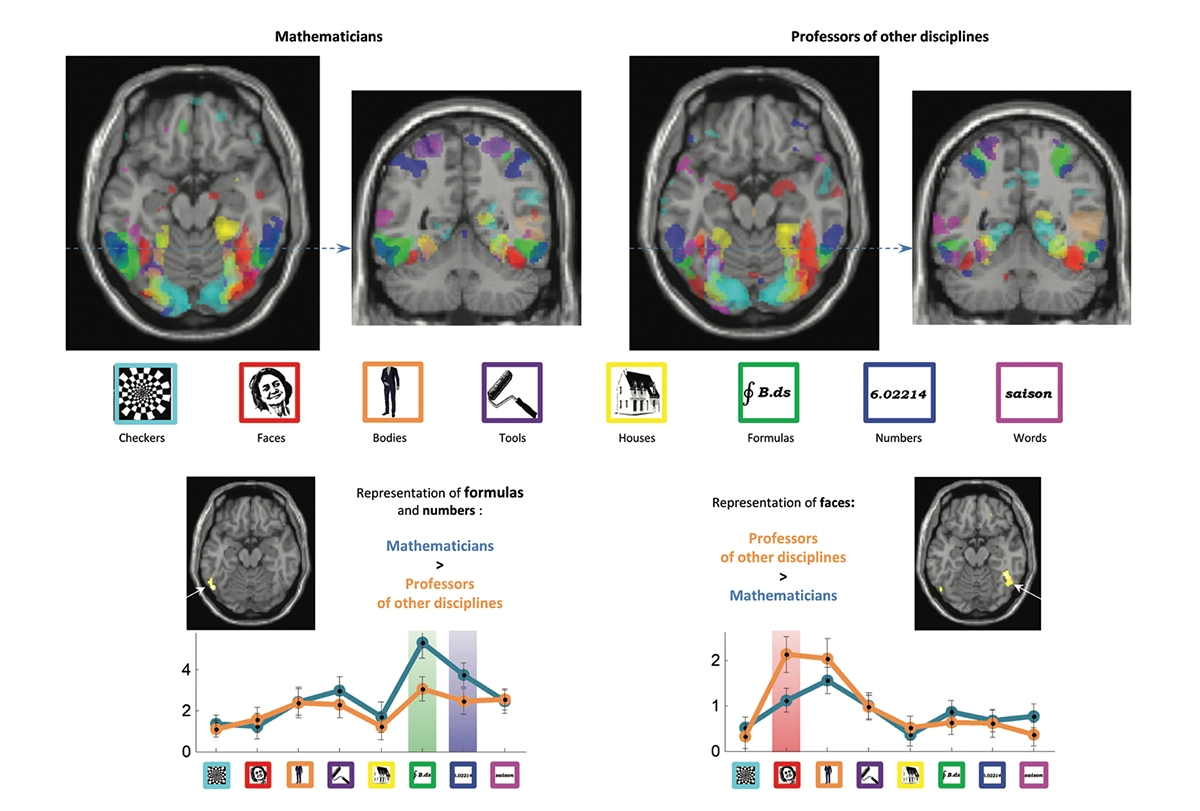
Formula flash: In visual areas in professional mathematicians, compared with professors of other disciplines, the activity of the inferotemporal region — which we all use to recognize numbers — almost doubles whenever a number or an equation is flashed, according to research by Marie Amalric and the author at the NeuroSpin Center in Saclay, France.
Reading mathematical formulas
Whoever learns mathematics also becomes an expert reader of a peculiar language: that of numbers and algebraic expressions. Do the following equations speak to your ears?

If so, you have recycled some of your visual areas for mathematical formulas. Using MRI, Marie Amalric and I mapped the visual cortex of mathematicians and nonmathematicians. We presented them with a broad variety of images: checkerboards, faces, body parts, houses, objects and written words, but also numbers and mathematical formulas.
As you can see here, learning mathematics does not fully scramble the mosaic of brain areas specialized for these different categories of images. Mathematicians and laypeople alike all possess similar areas for places, objects, words or faces, at roughly the same cortical sites. However, mathematicians differ from other people in two ways. First, in their brains, mathematical formulas occupy an inferotemporal region that we all use to recognize numbers. In mathematicians, compared to other participants, the activity of this region almost doubles whenever a number or an equation is flashed. Tightly connected to the parietal cortex, this site is used to manipulate all sorts of mathematical objects — and the more we know, the bigger it gets.
But an opposite difference also exists: Mathematicians show less brain activity than other people in the right hemisphere face area. This finding raises more questions than it solves. We do not know whether it has any functional consequences: Are mathematicians, on average, worse at recognizing faces, as many of us suspect? (I am a mathematician myself, and do find faces quite challenging.) Is this an effect of learning — do mathematicians become less sensitive to faces as they immerse themselves in abstruse equations? Or could it be a genetic effect, present even before school, and which biases some children to prefer the company of numbers? In the field of mathematics and its brain mechanisms, much remains to be discovered.
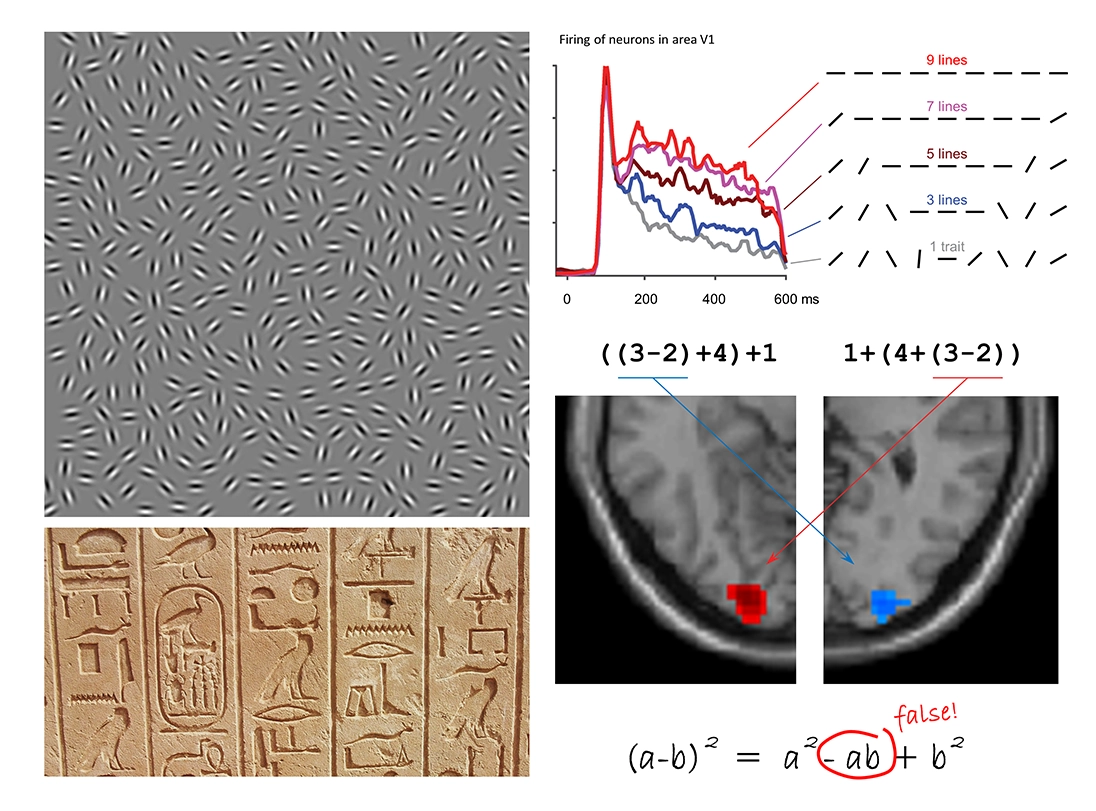
Homing in: Circling an image increases its saliency. In the primary visual area V1, late neuronal discharges increase as a function of the number of aligned bars, according to recordings from macaque monkey neurons in Charles Gilbert’s lab at Rockefeller University in New York City (top). Data collected on NeuroSpin’s 3-tesla MRI machine show that in humans, a single pair of parentheses suffices to evoke a similar effect: brain activity is amplified at the corresponding location in occipital cortex (bottom).

Recommended reading
What infant fMRI is revealing about the developing mind

Monkeys build mental maps to navigate new tasks

‘Into the wild’: Moving studies of memory and learning out of the lab
Explore more from The Transmitter
Snoozing dragons stir up ancient evidence of sleep’s dual nature

The Transmitter’s most-read neuroscience book excerpts of 2025
